<합성곱 신경망의 구조, 이제는 명확히 이해하자!>
● 오랜만에 뵙습니다. 합성곱 신경망(CNN)의 구조에 대해 간단히 살펴보도록 하겠습니다.
● 일반적인 신경망의 학습은 입력층에서 은닉층을 거쳐갈수록 점점 복잡한 특징들을 학습해나갑니다.
● 기본 특징(모서리나 직선 등)에서부터 조금 더 복잡한 패턴(원, 정사각형) 그리고 더 복잡한 추상화된 패턴(고양이 수염, 얼굴의 부분, 자전거 바퀴 등)에 이르기까지 말이죠.
● 합성곱 신경망 또한 이러한 일반적인 신경망의 학습과 별반 다르지 않게 진행됩니다. 오차를 계산하여 오차만큼 역전 파한 후, 가중치를 조정해가는 학습의 과정도 물론 동일합니다.
● 단, 하나! 일반 신경망에서는 특징의 학습을 전 결합층(Fully-Connected layer = MLP)에서 했다면, 합성곱 신경망에서는 합성곱층(Convolution layer)에서 한다는 것만 다릅니다.
● 딥러닝이 머신러닝과 갖는 차이점은 바로 특징 추출을 사람이 직접 하지 않아도 된다는 점이었습니다. 즉, 딥러닝(신경망)은 특징추출과 분류를 동시에 수행할 수 있는 고마운 존재입니다.
● 음(..) 그런데 이미지 학습에 있어서 전 결합층(MLP)의(MLP) 단점이 기억나시나요? 그것은 바로 1차원의 형태로 벡터 변환을 해서 입력해줘야 하기 때문에 데이터의 공간적 특징을 잃어버리는 것에 있었습니다.
● 그렇다면 전 결합층의 문제는 딥러닝의 주요 핵심 기능. 즉, 특징 추출(특징 학습)과 분류 중 특징 학습에 있다고 볼 수 있는 것이죠.
● 그렇다면 문제가 있는 부분은 개선하고, 문제가 없는 부분은 그대로 살려서 활용하면 좋을 것 같습니다.
● 즉, 특징 추출(특징 학습)은 지역적 연결을 가진 합성곱층에게 맡기고, 기존에 잘 수행하고 있던 분류의 역할은 그대로 전 결합층에게 맡겨보는 것입니다.
● 다음 글에서는 이 아이디어를 반영해서 구성된 일반적인 합성곱신경망을 크게 4개의 구조로 나누고, 각각의 부분이 수행하는 기능에 대해 마저 살펴보겠습니다.

● CNN의 구조는 크게 4부분으로 나눌 수 있습니다. 바로 입력층, 합성곱층, 전결합층, 출력층입니다.
● 각 구조를 명확히 이해하고 넘어갑시다. 입력층은 말 그대로 이미지를 입력하는 층입니다. 합성곱층에서는 특징의 추출 즉, 특징의 학습이 이루어집니다. 그다음 단계인 전 결합층에서는 분류를 담당합니다. 마지막 출력층은 분류 결과를 출력하는 층입니다.
● 위의 그림을 말로 풀어서 설명해보면 다음과 같습니다.
● 입력층에 손글씨 숫자 3이 들어옵니다. 이 이미지가 합성곱층에 들어오며 특징이 학습됩니다.
● 학습하여 발견된 패턴은 특징 맵(피처 맵)으로 추출되는데 점점 특징 추출의 단계가 진행될수록 이 특징 맵 이미지의 크기는 줄어들고, 특징 맵의 수(층의 깊이)는 계속 추가되는 것을 볼 수 있습니다.
● 아하! 합성곱층은 이미지의 결정적인 특징을 학습하는 추상화를 위한 공간이라고 생각하셔도 좋습니다.
● 이제 전결합층으로 갈 차례이군요. 학습의 결정체인 특징 벡터는 1차원으로 변환되어 전 결합층에 입력됩니다. 전결합층에서는 이 특징 벡터를 기반으로 이미지를 분류합니다.
● 분류 결과에 해당되는 출력층의 노드가 발화됩니다. 여기에서는 출력층의 노드 3과 7 둘 뿐이고, 이 중 3이 발화됩니다.
● 아, 대략 신경망의 구조와 전체적인 작동 과정이 머릿속에 그려지는 듯합니다..
● 그런데 말입니다? CNN의 핵심인 합성곱층에서 특징 추출(특징 학습)은 어떻게 일어나는 것일까요? 과연 어떻게 이미지에서 패턴을 학습하는 마법을 부리는 걸까요?
● 매우 중요하고도 좋은 질문입니다. 바로 다음 글에서 합성곱층에서 벌어지는 특징 추출의 마법을 더 자세히 들여다보고, 그 세부적인 원리들도 함께 파헤쳐보도록 하겠습니다.
<합성곱 신경망의 합성곱층에서는 어떤 일이 벌어지는 걸까?>
● 합성곱층은 합성곱 신경망의 핵심이라 할 수 있습니다. 왜냐하면 이곳에서 이미지 데이터의 특징을 추출해내기 때문이죠.
● 합성곱이란 무엇을 의미하는 것일까요?
● 합성곱은 수학에서는 두 함수를 인수로 해서 새로운 함수를 만들어내는 연산을 뜻합니다. 합성곱 신경망에서의 두 인수는 입력 이미지와 합성곱 필터를 의미한다 할 수 있습니다.
● 합성곱층이 이미지를 처리하는 과정을 함께 살펴봅시다.
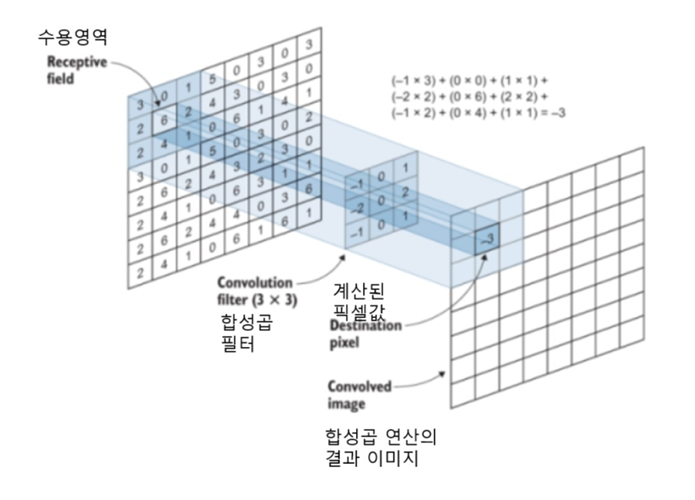
● 위 그림과 같이 가운데 위치한 3*3 크기의 행렬이 합성곱 필터입니다. 커널(Kernel)이라고 부르기도 합니다.
● 커널은 입력 이미지 위를 픽셀 단위로 움직여다니며 연산을 수행합니다. 각 위치에서 연산된 픽셀값을 모아 '합성곱 연산'을 수행한 새로운 이미지 즉, 특징 맵을 만들고 이를 다음 층으로 전달합니다. 이때 합성곱 연산이 한 번 수행되는 입력 이미지 상의 범위를 수용 영역이라고 부릅니다.

● 그런데 커널 값은 대체 무엇을 의미하는 것일까요? 신경망은 가중치를 학습하는 것이라 했습니다. 합성곱 신경망에서는 커널 즉, 이 합성곱 행렬이 가중치가 됩니다.
● 그럼 합성곱 행렬은 어떻게 정해지는 것일까요? 처음에는 무작위 값으로 초기화됩니다. 그런 다음 시간이 지나면서 신경망에 의해 학습이 된다고 이해하시면 좋습니다.
● 다층 퍼셉트론의 가중합(Weighted sum)이 기억나실겁니다. 바로 입력값과 각각의 입력값에 상응하는 가중치 값들을 곱해준 후, 그 결과들을 모두 합한 값 말입니다.

● CNN에서도 마찬가지입니다. 입력값은 수용 영역 안에 들어와 있는 각각의 입력 픽셀 값이고,, 가중치는 합성곱 필터의 픽셀 값이라 생각하면 이해가 쉽습니다.
● 아래 그림과 같이 수용영역과 합성곱 필터가 겹치는 픽셀 값을 각각 곱해주고, 그 결과를 합해줍니다. 그런 다음 그 결과 값을 필터 중심에 해당하는 픽셀 위치의 값으로 넣어 특징 맵을 완성해나가는 것입니다.

'인공지능 (AI)' 카테고리의 다른 글
| 35번째 이야기 - 커널 사이즈, 스트라이드, 패딩, 합성곱 신경망 (1) | 2024.06.02 |
|---|---|
| 34번째 이야기 - 합성곱, 커널, 입력 이미지, 가중합, 합성곱층 (0) | 2024.06.02 |
| 32번째 이야기 - 다중퍼셉트론, MLP, 합성곱 신경망, CNN, 다중퍼셉트론 단점 (0) | 2022.11.21 |
| 31번째 이야기 - 모의 담금질(Simulated Annealing) 알고리즘, 경사하강법, gradient descent (0) | 2022.11.21 |
| 30번째 이야기 - 오토인코더, autoencoder, 경사하강법, 평균제곱오차, mse (0) | 2022.11.21 |




댓글