<다층 퍼셉트론(MLP)으로(MLP) 이미지를 다룰 때 나타나는 단점 2가지>
● 다층 퍼셉트론(MLP)의 학습이 오차 역전파와 ReLU 활성화 함수의 도입으로 수월해지게 되면서 MLP를 활용한 다양한 실생활의 문제 해결 적용의 시도가 시작됩니다.
● 신경망으로 2차원의 이미지 분류를 하려는 작업 또한 그 시도들 안에 포함되어 있었습니다. 신경망으로 2차원의 이미지를 다루기 위해서는 신경망이 요구하는 형태로 전처리(변환)하는 과정이 필요합니다.
● 이를 이해하기 위해서는 컴퓨터가 어떻게 이미지를 인식하는지 살펴볼 필요가 있습니다.
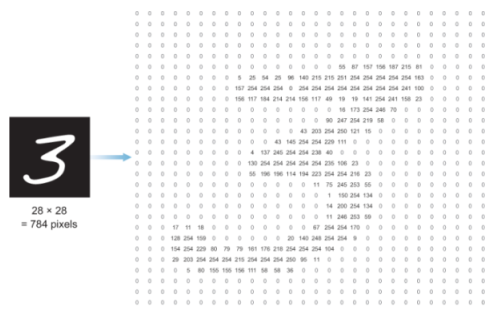
● 보시는 바와 같이 여기 28*28 크기의 2차원 이미지가 있습니다. 자세히 보면 각 픽셀의 값은 0~255의 값을 가집니다(0은 검은색, 255는 흰색).
● MLP는 1행 n열의 1차원 행렬의 벡터만 입력받습니다. 아래 그림과 같이 4개의 행으로 이루어진 왼쪽의 사각형 픽셀 값들을 오른쪽과 같이 한 줄로 변환해주어야만 입력을 받을 수 있다는 의미입니다. 이를 Image flattening(이미지 벡터 변환)이라고 부릅니다.

● 여기서 픽셀의 검은색이 0, 흰색이 255라면 입력 벡터는 다음과 같습니다.

● 위의 손글씨 숫자 '3' 이미지가 갖고 있는 픽셀의 수는 몇 개일까요?? 네, 28*28=784개입니다. 즉, 이를 신경망에 넣고 처리하려면 1*784 형태의 1차원 벡터로 변환해주어야 합니다. 즉, 신경망의 입력층에 들어갈 노드는 x1, x2, x3,..... x784가 일렬로 이루어진 784개가 되겠죠.
● 이러한 이유로 케라스 라이브러리를 사용하여 신경망 코드를 입력할 때, Flatten 층을 임포트합니다.

● 그런데 말입니다. 여기서 심각한 문제가 발생합니다. 2차원 벡터의 이미지를 1차원 벡터로 변환하게 되면 어떤 정보가 손실되지 않을까 하는 합리적인 의심이 들 수 있습니다.
● 네, 이 의심은 타당합니다. 사실, 차원의 수를 줄이게 되면 당연히 정보 손실이 일어납니다. 2차원의 정보를 모두 폐기하게 되는 것과 다름없기 때문이죠. 여기에서는 이미지 내 공간적 특징이 손실됩니다.
● 즉, 2차원의 이미지를 이렇게 차원 축소해버리면 서로 인접한 픽셀 간의 관계 정보가 사라집니다. MLP는 픽셀들이 서로 어떠한 연결성을 갖고 있었다는 사실을 유추해낼 수 없습니다. 이 점이 MLP로 이미지를 다룰 때의 큰 단점입니다.

● 위와 같은 그림에서 1이 검은색, 0이 흰색이라고 했을 경우, 위의 왼쪽 그림과 같이 x1, x2, x5, x6이 발화했을 때만 정사각형을 인식할 수 있습니다. 그러나 옆의 2개의 그림과 같이 정사각형의 모양과 위치가 달라지면요? 이미지 내 다양한 자리에 위치한 정사각형을 MLP는 알아차리지 못합니다.
● 결국 이 MLP가 다양한 자리에 위치한 정사각형을 알아차리는 능력을 가지려면 이미지 내 모든 자리에 위치한 정사각형의 이미지가 필요합니다만 너무 문제가 복잡해지고, 그냥 사람이 분류하는 편이 낫습니다(...)
● 결국 중요한 건 이미지를 구성하는 픽셀 간의 관계입니다.
● 또 한 가지 단점은 뭘까요? 다음 글에서 이를 마저 살펴보고, 이 2가지 단점을 극복하기 위해 등장한 설루션인 CNN(합성곱신경망)CNN(합성곱 신경망)에 대해 살펴보도록 하죠.
<다층 퍼셉트론(MLP)으로(MLP) 이미지를 다룰 때 나타나는 단점 2가지>
● MLP로 이미지를 다루게 되면 나타나는 또 한 가지 단점은 뭘까요? 그것은 바로 계산의 복잡도입니다.
● 방금 우리가 다뤄본 손글씨 숫자 '3'은 28*28 크기의 이미지였기 때문에 사실 그렇게 문제가 되지 않습니다. 하지만 큰 이미지일 경우에는 문제가 됩니다.
● 1280*7841280*784 크기의 이미지일 경우 이 입력층에 연결된 은닉층 하나의 노드마다 1,003,520개의 파라미터를 갖게 될 겁니다. 계산 복잡도의 측면에서 실로 우리가 통제할 수 있는 범위를 넘어섭니다.
● 공간적 특징의 손실과 계산 복잡도의 문제는 바로 이미지를 처리할 때 MLP가 갖는 치명적인 단점이었습니다. 그렇다면 해결책은 없을까요?
● 1280*7841280*784 크기의 이미지일 경우 이 입력층에 연결된 은닉층 하나의 노드마다 1,003,520개의 파라미터를 갖게 될 겁니다. 계산 복잡도의 측면에서 실로 우리가 통제할 수 있는 범위를 넘어섭니다.
● 공간적 특징의 손실과 계산 복잡도의 문제는 바로 이미지를 처리할 때 MLP가 갖는 치명적인 단점이었습니다. 그렇다면 해결책은 없을까요?
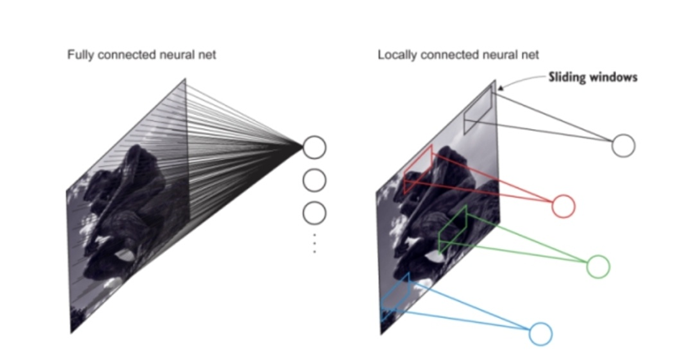
● 위의 그림에서 보시는 바와 같이 MLP는 모든 노드가 Fully-connected(전결합) 되어 있습니다. 그러나 CNN은 지역적으로 연결된(locally connected) 구조를 갖습니다. 그러다 보니 전 결합된MLP에 비해 파라미터의 개수가 현저히 적습니다.
● 정리해봅시다. 2차원의 이미지를 1차원 벡터로 변환하게 되면 반드시 발생하게 되는 공간 정보의 손실과 전 결합층의 특성을 갖는 MLP가 갖는 계산 복잡도를 고려하면 다른 대안을 갖는 신경망이 필요합니다.
● 즉, 2차원의 공간적 특징을 간직하면서도 계산 복잡도를 줄여주는 그런 신경망 말이죠.
● 바로 이 지점이 CNN이 빛을 발하는 지점입니다. 정리하면 CNN은 2차원의 이미지 백터를 그대로 입력받을 수 있어 공간적 특징을 학습할 수 있도록 설계되었습니다. 또 지역적으로 연결된 구조로 계산 복잡도를 현저히 낮춰줍니다.
● 이렇게 살펴보니 이미지 처리에 특화된 신경망인 CNN이 최초의 딥러닝 알고리즘이라고까지 불리는 그 위상을 이해할 수 있을 것만 같습니다.
'인공지능 (AI)' 카테고리의 다른 글
| 34번째 이야기 - 합성곱, 커널, 입력 이미지, 가중합, 합성곱층 (0) | 2024.06.02 |
|---|---|
| 33번째 이야기 - 합성곱 신경망, CNN, 합성곱층, Convolution layer (0) | 2022.11.21 |
| 31번째 이야기 - 모의 담금질(Simulated Annealing) 알고리즘, 경사하강법, gradient descent (0) | 2022.11.21 |
| 30번째 이야기 - 오토인코더, autoencoder, 경사하강법, 평균제곱오차, mse (0) | 2022.11.21 |
| 29번째 이야기 - 머신러닝, 기계학습, 준지도학습, 자기주도학습 (0) | 2022.11.21 |




댓글